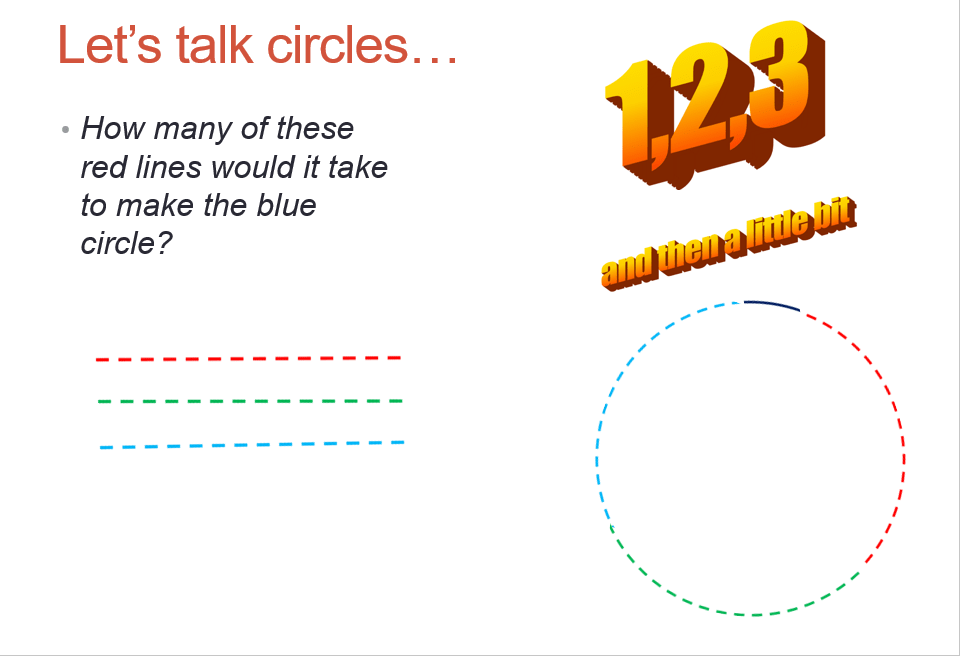
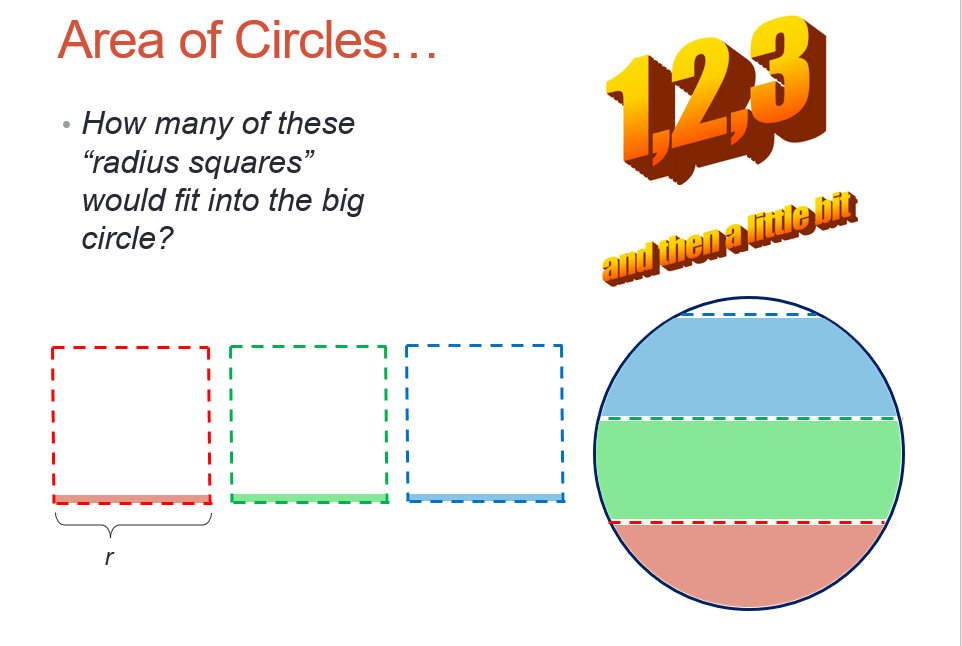
Color-by-number! With my writing, I have been playing around with ways to make the answer to a math problem something that is more interactive. Color by number is one thing that I stumbled upon last year, and I think it’s got some mad potential for older learners. (I freely admit that I am not the first teacher to create this. There are lots of TPT resources and freebies online, but they are generally reserved for younger grades and practicing basic operations. This resource I built out for my 8th graders practicing equations. The image is from a google image search and not my own):
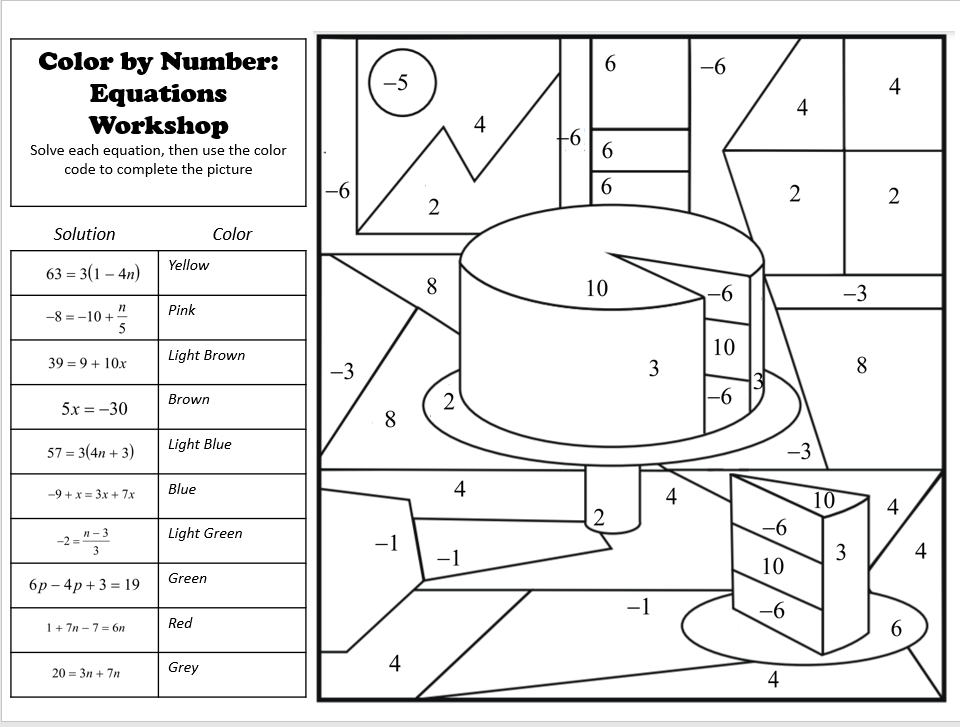
The equations that students must solve are presented on the left. Once they solve an equation, they can color in the spaces with the corresponding color. (For example, the solution to 63=3(1-4n) is -5, so any space with a -5 on it should get colored in yellow.)
I used it as a part of a review project after we had spent a couple weeks solving equations. I put out a big bowl of colored pencils and let them dig in. took about 35 minutes to complete.
I also spent a two days where students built their own color by number math art. I gave parameters for the types of problems that they used, and asked them to build something creative. Some were better than others, but I absolutely need to share this color by number piece from Luz, cuz it rips.

It’s Pluto with some of the members of k-pop band BTS. Why are they all together? Ask Luz.
I’ve been sitting on this post for a WHILE because it is going to be a big part of my new Choose Your Own Adventure book, Fraction Action: Double Feature, and I didn’t want you vultures to steal all my good ideas 😉
Here is a downloadable pdf version of the “equations workshop” sheet shown above, and it has the problems in bigger boxes to be printed on the back.
Here is the powerpoint version if you want to add math that works better with your students! Enjoy!